Abstracts and Abstraction
The Abstraction Principle states:
A client should be able to use a function (class or module) without knowing how it's implemented. Conversly, a provider should be able to modify the implementation of a function (class or module) without worrying about breaking client code.
A language supports the Abstraction Principle by allowing programmers to separate the description of a computation (implementation) from its execution (use).
In effect, when a programmer declares a function or procedure:
int square(int x) { return x * x; }
he's describing a computation:
x * x
However, the computation isn't executed at this point. That happens later when the function is called:
square(2 + 3); // = 25
square(2 * 2); // = 16
Note that the function can be called many times, even though it only needs to be described once.
Abstracts
Abstracts in Epsilon
In Epsilon an abstract is an expression:
<Expression> ::= <Abstract> | <FunCall> | etc.
<Command> ::= <ProcCall> | etc.
<Abstract> ::= <ExpAbstract> | <CmmdAbstract>
<ExpAbstract> ::= (fun (<Symbol>*) <Expression>)
<CmmdAbstract> ::= (proc (<Symbol>*) <Command>)
Here's a sample interaction with Epsilon's VMConsole. User input is shown in boldface:
-> [const square (fun (x) (* x x))]
done
-> [var x 0]
done
-> [const inc (proc (y) {assign x (+ x y)})]
done
-> {inc (square 3)}
ok
-> x
9
-> [const addx (fun (x) (fun (y) (+ x y)))]
done
-> [const add3 (addx 3)]
done
-> (add3 4)
7
The value of an expression abstract is a function. The value of a procedure abstract is a procedure. For example, evaluating the expression:
(fun (x y) (+ x y))
produces a function object as a value. For now, we represent this object by the string:
<Function (x y) (+ x y)>
Thus, the declaration:
[const add (fun (x y) (+ x y))]
creates the binding:
add = <Function (x y) (+ x y)>
We might represent functions internally as instances of a Function class:
class Function {
protected Expression body;
protected List params;
public Object apply(List args, Context context) {
1. context.push();
2. for each param in params and arg in
args:
context.put(param,
arg);
3. result = body.eval(context);
4. context.pop();
5. return result;
}
}
Scheme's Lambda Operator
<Lambda> ::= (lambda (<Parameter>*) <Expression>+)
(define square (lambda (x) (* x x)))
Haskell's Lambda Operator
square = \x->x*x
Mixed Abstracts in C
int square(int x) { return x * x; }
void accum(int x)
{
int y = 100;
total = x + y;
}
Generics in C++ (Templates)
There's no reason why the body of an abstract can't be a declaration. The value of a declaration abstract is called a generic. In C++ generics are called templates. For example, the swap function only swaps integer variables. We'll need to define another swap function to swap doubles or strings or employee records. We can define all of these swap functions in one definition by declaring the type of the parameters to also be a parameter!
template
<typename Data>
void swap(Data *x, Data *y)
{
Data temp = *x;
*x = *y;
*y = temp;
}
(The "class" keyword can be used instead of "typename".) When the C++ compiler sees a call to swap, it determines the type of the arguments and automatically generates definitions of the needed swap variants. For example, when C++ compiles:
int
main()
{
int a = 42, b = 35;
swap(&a, &b); // ok
string u = "hello", v = "goodbye";
swap(&u, &v); // ok
return 0;
}
It automatically generates the definitions:
void
swap(int *x, int *y)
{
int temp = *x;
*x = *y;
*y = temp;
}
and
void
swap(string *x, string *y)
{
string temp = *x;
*x = *y;
*y = temp;
}
Each time the generic is elaborated (i.e., each time the template is instantiated) a new function is declared (by the compiler).
Function Call Evaluation Algorithms/Parameter Passing Mechanisms
Terminology: Parameters, Operands, and Arguments
Assume the following function has been declared:
int f(int x, int y) { return 2 * x + y; }
The signature or type of f is:
int f(int x, int y)
The body of f is:
{ return 2 * x + y; }
The parameters of f are x and y.
Assume the following function call is made:
f(2 + 3, 4 * 5);
This type of expression is called a function call or application. The operands are:
2 + 3
4 * 5
The arguments are 5 and 20.
Types of Evaluation Algorithms
Assume the declaration of f is:
T f(T1 x1, ..., Tn xn) { body }
Assume the following function call must be evaluated:
fcall = f(e1, ..., en)
where e1, ..., en are unevaluated operands.
For example, if f is:
int f(int x1, int x2) { return 2 * x1 + x2; }
then
body = return 2 * x1 + x2;
If
fcall = f(2 + 3, 2 * 2)
then
e1 = 2 + 3
e2 = 2 * 2
We are interested in algorithms that implement the function:
Value eval(FunCall fcall, Context context) {
// now what?
}
We might want to start by gathering the pieces together:
Value eval(FunCall fcall, Context context) {
List operands = [e1, ..., en] =
fcall.getOperands();
List params = [x1, ..., xn] =
f.getParams();
Expression body = f.getBody();
// now what?
}
Here's a breakdown of the algorithms we will describe. The lazy algorithms (i.e., algorithms that only evaluate the operands they need) are marked:
Substitution Algorithms
Applicative Order
Normal Order (lazy)
Environmental Algorithms (these require an environment)
Pass-by-value (also called eager)
Pass-by-text
Pass-by-name (lazy)
Pass-by-reference
Substitution Algorithms
Normal Order Evaluation (Lazy)
In normal order evaluation, we replace the parameters that occur in the body of the function by the corresponding unevaluated operands, then recursively evaluate the modified body.
Value eval(FunCall fcall, Context context) {
List operands = [e1, ..., en] =
fcall.getOperands();
List params = [x1, ..., xn] =
f.getParams();
Expression body = f.getBody();
// normal order:
1. for ei in operands
replace xi by
ei in body
2. result = eval(body, context)
3. return result
}
For example, if f is:
int f(int x1, int x2) { return 2 * x1 + x2; }
and
fcall = f(2 + 3, 2 * 2)
then
body = return 2 * x1 + x2;
before step 1. After step 1:
body = return 2 * (2 + 3) + (2 * 2);
Recursively evaluating the body produces 14 as the result.
Notice that this is lazy. For example, if
body = return 2 * x1;
then there is no substitution for 2 * 2, hence 2 * 2 will never be evaluated.
Note 1: C++ uses eager or pass-by-value evaluation normally, however, if we declare a function to be inline:
inline int f(int x1, int x2) { return 2 * x1 + x2; }
then C++ uses a substitution algorithm to evaluate calls to f.
Note 2: C and C++ allow programmers to declare macros:
#define min(x, y) x<y?x:y
The C/C++ pre-processor replaces all macro calls using normal-order evaluation. For example, the pre-processor replaces the line:
min(2 + 3, 2 * 2)
with the line:
2 + 3?2 + 3:2 * 2
Environmental Algorithms
Eager: Pass-by-value (constant parameters)
In pass-by-value or eager evaluation, all operands are eagerly evaluated-- needed or not. This produces a list of values called arguments. Temporary bindings between parameters and corresponding arguments are placed in the context's environment. The body of the function is evaluated relative to the context. As parameters are encountered in the body, we should be able to find bindings to the corresponding arguments in the context.
Value eval(FunCall fcall, Context context) {
List operands = [e1, ..., en] =
fcall.getOperands();
List params = [x1, ..., xn] =
f.getParams();
Expression body = f.getBody();
// eager:
1. for ei in operands
argi = eval(ei,
context)
2. context.push(); // push a new frame on environment stack
3. for each xi in params
context.put(xi,
argi)
4. result = eval(body, context)
5. context.pop(); // get rid of param bindings
6. return result
}
For example, if f is:
int f(int x1, int x2) { return 2 * x1 + x2; }
and
fcall = f(2 + 3, 2 * 2)
then
arg1 = eval(2 + 3, context) = 5
arg2 = eval(2 * 2, context) = 4
The bindings:
x1 = 5
x2 = 4
are placed in a temporary frame:
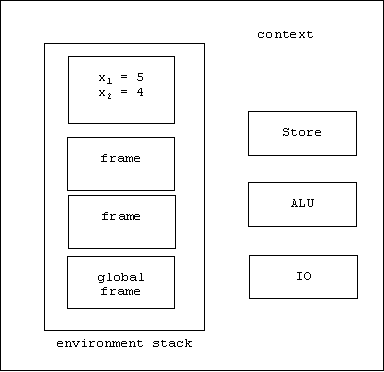
The body
return 2 * x1 + x2;
is evaluated relative to this context. This produces 14 as a result. The temporary frame is popped off of the stack.
Pass-by-text
Pass-by-text is similar to pass-by-value in structure, only the parameters are bound to the unevaluated operands rather then their values:
Value eval(FunCall fcall, Context context) {
List operands = [e1, ..., en] =
fcall.getOperands();
List params = [x1, ..., xn] =
f.getParams();
Expression body = f.getBody();
// pass-by-text:
1. context.push(); // push a new frame on environment stack
2. for each xi in params
context.put(xi,
ei)
3. result = eval(body, context)
4. context.pop(); // get rid of param bindings
5. return result
}
Now that expressions are bindables, the evaluation algorithm for symbols needs to be modified slightly:
Value eval(Symbol symbol, Context context) {
1. val = context.get(symbol)
2. if (val is an expression) val = eval(val, context);
3. return val
}
For example, if f is:
int f(int x1, int x2) { return 2 * x1 + x2; }
and
fcall = f(2 + 3, 2 * 2)
then the bindings:
x1 = 2 + 3
x2 = 2 * 2
are placed in a temporary frame:
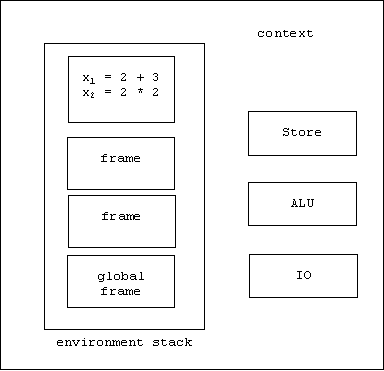
Evaluating the body of f causes us to evaluate the symbols x1 and x2. When we look these up in the environment, we discover they are bound to expressions, not values, hence we must perform an additional evaluation to get the arguments.
Notice that pass-by-text is lazy because if x2 doesn't occur in the body, then the corresponding operand, 2 * 2, never gets evaluated.
Thunks
A thunk is a parameterless function. For example:
int thunk() { return 2 + 3; }
Thunks are also called promises.
Creating a thunk out of an expression is also called freezing or delaying the expression.
Of course each time the thunk is called, the same value is produced:
thunk(); // = 5
thunk(); // = 5
etc.
Calling a thunk is also called thawing or forcing the thunk.
Thunks can be inefficient. Each time a thunk is thawed, the same expression needs to be re-evaluated. Even though it produces the same value each time. We can eliminate this inefficiency using memoized thunks. A memoized thunk caches its value after the first time it is thawed:
int memoizedThunk() {
static int cache = 0;
static bool firstCall = true;
if (firstCall) {
firstCall = false;
cache = 2 + 3; // eval once
}
return cache;
}
(Recall: static local variables in C/C++ retain their values across function calls. How would you do this in Java?)
Lazy: Pass-by-name
Pass-by-text is similar to pass-by-text, only the parameters are bound to frozen operands rather than the operands themselves:
Value eval(FunCall fcall, Context context) {
List operands = [e1, ..., en] =
fcall.getOperands();
List params = [x1, ..., xn] =
f.getParams();
Expression body = f.getBody();
// by-name:
1. for ei in operands
let thunki =
freeze ei // i.e., Value thunki() { return ei;
}
2. context.push(); // push a new frame on environment stack
3. for each xi in params
context.put(xi,
thunki)
4. result = eval(body, context)
5. context.pop(); // get rid of param bindings
6. return result
}
Now that thunks are bindables, the evaluation algorithm for symbols needs to be modified slightly so that it thaws thunks if necessary:
Value eval(Symbol symbol, Context context) {
1. val = context.get(symbol)
2. if (val is a thunk) val = eval(val(), context);
3. return val
}
For example, if f is:
int f(int x1, int x2) { return 2 * x1 + x2; }
and
fcall = f(2 + 3, 2 * 2)
then the thunks:
int thunk1() { return 2 + 3; }
int thunk2() { return 2 * 2; }
are created, and the bindings:
x1 = thunk1
x2 = thunk2
are placed in a temporary frame:
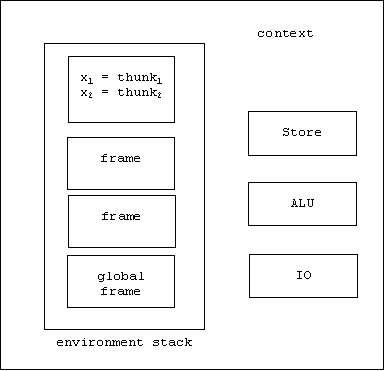
Evaluating the body of f causes us to evaluate the symbols x1 and x2. When we look these up in the environment, we discover they are bound to thunks which must first be thawed. Of course thawing them produces 5 and 4, hence the value of the call is 14.
Notice that pass-by-name is lazy because if x2 doesn't occur in the body, then the corresponding operand, 2 * 2, never gets evaluated.
Pass-by-reference
Define the reference of an expression as follows:
ref(symbol, context) = context.environment.get(symbol)
ref(exp, context) = eval(exp, context), otherwise
In other words, the reference of an expression is simply its value unless the expression happens to be the name of a variable. In this case its the location that the symbol is bound to in the environment. We don't bother accessing the store.
The de-referencing operator completes the evaluation job:
deref(location, context) = context.store[location]
deref(val, context) = val, otherwise
Pass-by-reference is similar to pass-by-value, only the parameters are bound to the corresponding operand reference instead of its value:
Value eval(FunCall fcall, Context context) {
List operands = [e1, ..., en] =
fcall.getOperands();
List params = [x1, ..., xn] =
f.getParams();
Expression body = f.getBody();
// pass-by-reference:
1. for ei in operands
argi = ref(ei,
context)
2. context.push(); // push a new frame on environment stack
3. for each xi in params
context.put(xi,
argi)
4. result = eval(body, context)
5. context.pop(); // get rid of param bindings
6. return result
}
Now that references are bindables, the evaluation algorithm for symbols needs to be modified slightly so that it dereferences references if necessary:
Value eval(Symbol symbol, Context context) {
return deref(context.get(symbol), context);
}
For example, if f is:
int f(int x1, int x2) { return 2 * x1++ + x2++; }
and the following variables have been declared:
int a = 20;
int b = 10;
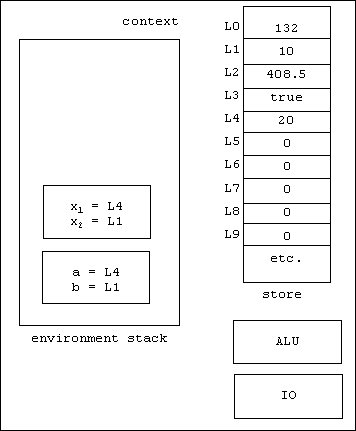
Here's the context at this point. Note that the global frame contains bindings of a to the location L4 and b to the location L1:
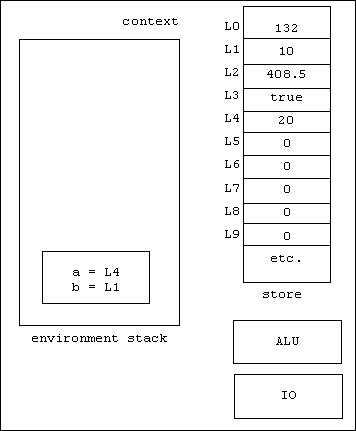
Now assume we want to evaluate the call:
fcall = f(a, b)
then
arg1 = ref(a, context) = L4
arg2 = ref(b, context) = L1
The bindings:
x1 = L4
x2 = L1
are placed in a temporary frame:
The body
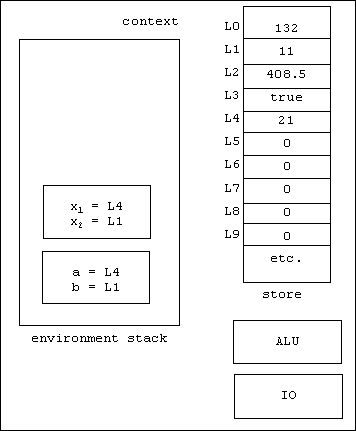
return 2 * x1++ + x2++;
is evaluated relative to this context, producing the value 50, but incrementing x1 and x2 as a side effect. Since x1 and x2 are references to a and b, a and b are also incremented:
Here's a snapshot of the context just before the temporary frame is then popped off of the stack:
Mutator
A mutator is a function that modifies its callers environment. In the example above, f is a mutator because it modifies a and b which belong to the caller. Mutators often employ pass-by-reference.
// mutator?
void swap(int x, int y)
{
int temp = x;
x = y;
y = temp;
}
void main()
{
int a = 10;
int b = 20;
swap(a, b);
print(a); // prints 10
print(b); // prints 20
}
To make this work we must specify pass-by-reference:
// mutator?
void swap(int& x, int& y)
{
int temp = x;
x = y;
y = temp;
}
Aliasing Problems
Will the caller of f be surprised to find his variables, a and b, have been incremented? Hopefully not, but probably yes. Notice that this wouldn't have happened if pass-by-value had been used. In this case the bindings
x1 = 20
x2 = 10
would have been pushed on the stack. Of course incrementing a constant may not make sense, but a and b definitely won't be incremented.
Eager: Pass-by-value (variable parameters)
How can parameters be updated if they are bound to constants? To make sense out of this, most languages implement a variant of pass-by-value in which the parameters are bound to locations of freshly allocated variables. The arguments are then copied to these variables. Just before the result is returned by eval(), these variables are de-allocated.
To handle the efficient allocating and de-allocating of temporary variables, a section of the store is reserved for them. This section is called the call stack. A stack pointer is added to the context. It contains the location of the next available cell in the call stack. Temporary variables are allocated through the stack pointer:
x1 = context.sp++;
x2 = context.sp++;
De-allocating temporary variables is simply a matter of decrementing the stack pointer:
--sp;
--sp;
Pass-by-value versus Pass-by-reference in Scheme
In Scheme, primitive values such as numbers, characters, and Booleans are passed by value (variable version). Composite values such as lists, strings, and vectors are passed by reference.
Pass-by-value versus Pass-by-reference in C++
In C++ all values are passed by value. This can be inefficient when arguments are large objects. For example, assume the following function is declared:
void print(Employee emp) {
print(emp.name);
print(emp.salary);
print(emp.ssn);
}
The call:
print(smith)
makes and assigns a copy of smith to emp.
C++ allows programmers to request pass-by-reference for certain parameters:
void print(Employee& emp) {
print(emp.name);
print(emp.salary);
print(emp.ssn);
}
Now a reference to smith is assigned to emp:
emp = ref(smith)
Of course users will be nervous about calling this function. What if it accidentally sets emp.salary to $0? To put these people at ease, C++ also allows programmers to specify that a parameter should be passed by constant reference:
void print(const Employee& emp) {
print(emp.name);
print(emp.salary);
print(emp.ssn);
}
Now any possible change to emp inside of print() will result in a compiler error.
Pass-by-value versus Pass-by-reference in Java
In Java, primitive values such as numbers, characters, and booleans are passed by value (variable version). Composite values such as objects and arrays are passed by reference.
class Employee {
String name;
double salary;
}
class Test {
static void test(int x, Employee e) {
x = x + 10;
e.salary = 0;
}
static void main() {
Employee a = new Employee();
a.salary = 100000;
int b = 10;
test(b, a);
print(a.salary); // prints 0
print(b); // prints 10
}
}
Locating non-local references: Scope Rules
Consider the following declarations that occur in a package called math.lib:
double delta = 1e-10;
bool isSmall(double x) {
return abs(x) <= delta;
}
Suppose a user purchases math.lib and calls the isSmall() function in the following context:
void foo() {
double delta = 100;
double num = 50;
if (isSmall(num)) error("this number is too
small");
// etc.
}
What will happen when the call to isSmall() is evaluated. assume eager evaluation is used. Then the temporary binding:
x = 50
will be pushed on the environment stach, and the body of isSmall() will be evaluated:
result = eval("abs(x) <= delta", context);
During the evaluation of this expression several symbols will need to be evaluated:
eval(x, context) = 50
eval(abs, context) = <Function ... >
eval(<=, context) = <Function ... >
eval(delta, context) = ?
Obviously, a binding for delta won't be found in the top-most frame on the stack, because delta is an example of a non-local symbol: it's used but not defined by isSmall(). Where should we search for the values of non-local symbols?
Here's a snapshot of the context at this point. Notice that there are two delta bindings:
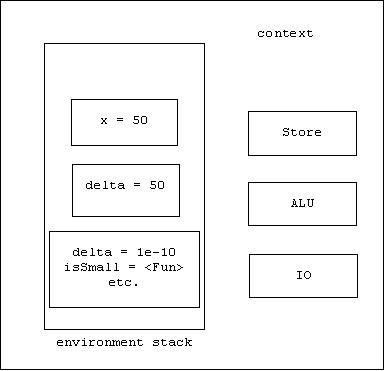
Scope Rules
The Dynamic Scope Rule says:
Search for the values of non-local symbols in the calling environment.
The Static Scope Rule says:
Search for the values of non-local symbols in the defining environment.
Both rules are used, but notice that the Static Scope Rule produces the right answer in this case, because the defining environment for isSmall() is the frame that also contains the correct binding for delta.
Local Functions
Closures
A closure is a function or procedure object that retains a pointer to its defining environment:
<FunClosure (x y) (+ x y) defEnv>
The Environment as a Frame Tree
Pass-by-Text versus Pass-by-Name
Appendix
The Correspondence Principle
Applicative Order Evaluation (Eager)
Not covered