Priority Queues

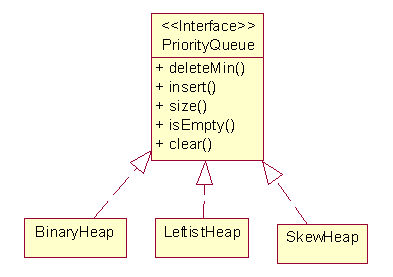
interface PriorityQueue {
Comparable deleteMin() throws EmptyQueueException;
void insert(Comparable x);
boolean isEmpty();
boolean size();
void clear();
}

A binary heap is a complete binary tree except possibly for the bottom level. The element of every node is greater than the element of its parent.

class BinaryHeap implements PriorityQueue {
Comparable[] elems = new Comparable[256];
int size = 0;
void insert(Comparable x) {
// percolate "hole" up until x fits
if (256 <= size) throw new OverflowError();
int hole = ++size;
for(; hole > 1 && x.compareTo(elems[hole/2]) < 0); hole /= 2)
elems[hole] = elems[hole/2];
elems[hole] = x;
}
public Comparable deleteMin() {
if( isEmpty()) return null;
Comparable minItem = findMin( );
elems[ 1 ] = elems[size--];
percolateDown( 1 );
return minItem;
}
private void percolateDown( int hole ) {
int child;
Comparable tmp = elems[ hole ];
for( ; hole * 2 <= size; hole = child ) {
child = hole * 2;
if( child != size &&
elems[ child + 1 ].compareTo( elems[ child ] ) < 0 )
child++;
if( elems[ child ].compareTo( tmp ) < 0 )
elems[ hole ] = elems[ child ];
else
break;
}
elems[ hole ] = tmp;
}
}

elems[i].left = elems[2*i]
elems[i].right = elems[2 * i + 1]
elems[i].parent = elems[floor(i/2)]

Applications

Selection

Find the kth largest element in an array:

int findKth(int[] a, int k) {

}

Put a[i] into a priorityQueue, then do k deleteMins.

Event Simulation

Assume k tellers are available initially.

There are two types of events, customer arrivals, and customer departures. Here is a crude sketch:

class BankSimulation {
Queue waiters;
int clock;
PriorityQueue events;
void run() {
while (!events.isEmpty()) {
Event e = events.deleteMin();
if (e instanceOf ArrivalEvent) {
clock = e.arrivalTime;
if (0 < availableTellers)
availableTellers--;
else
waiters.enqueue(e);
} else {
clock = e.departureTime;
if (!waiters.isEmpty()) {
ArrivaelEvent e = waiters.dequeue();
events.insert(new DepartureEvent(clock + e.duration);
} else {
availableTellers++;
}
}
}
}
}