Complexity

We often hear programmers and marketing executives brag that their program is superior to competing programs, even when the feature sets are virtually identical. Is there some mathematical basis for comparing the efficiencies of two programs?

Defining the complexity of algorithms, programs, and functions

Assume algorithm A implements function F. Assume we encode A as program P:

Implements(A, F) && Encodes(P, A)

There are four popular ways to measure the complexity of A:

T_A(N) = Worst case runtime complexity = The maximum number of steps of P that will be executed given any input of size N, not including the time required to read the input.

t_A(N) = Average case runtime complexity = The average number of steps of P that will be executed given any input of size N, not including the time required to read the input.

S_A(N) = Worst case space complexity = The maximum number of words of memory used by P when executed given any input of size N, not including the space required to store the input.

s_A(N) = Average case space complexity = The average number of words of memory used by P when executed given any input of size N, not including the space required to store the input.

Algorithm Analysis Rules

Here are a few rules for computing the complexity of an algorithm:

Expressions

STEPS(EXP1 OPERATION EXP2) = 1 + STEPS(EXP1) + STEPS(EXP2)
STEPS(f(EXP)) = STEPS(EXP) + T_A(N)
STEPS(CONSTANT) = 0
STEPS(VARIABLE) = 0

Where N is the size of the value of EXP and A is the algorithms that implements f.

Simple Statements

STEPS(VAR = EXP) = 1 + STEPS(EXP)
STEPS(return EXP) = STEPS(EXP)
STEPS(goto LABEL) = STEPS(continue) = STEPS(break) = 1

Loops

STEPS[for(i = 0; i < n; i++) STMT] = n * STEPS[STMT]

Conditionals

STEPS[if(COND) STMT1; else STMT2] = STEPS[COND] + max(STEPS[STMT1], STEPS[STMT2])

Sequences

STEPS[{STMT1; STMT2;}] = STEPS[STMT1] + STEPS[STMT2]

Estimating complexity

Notice that we are really defining the complexity of P rather than A. It might make more sense to write:

T_P(N), t_P(N), S_P(N), and s_P(N)

Certainly algorithm A might be encoded by programs P1 and P2 that contain different numbers of steps. For example, P1 might be a very long assembly language program while P2 might be a very short program written in some high-level language. In this case we would expect T_P1(N) to be different from T_P2(N).

In the end, we will be estimating the complexity of an algorithm rather than computing its exact complexity. When N is large, the margin of error in our estimate will generally be greater than the differences between T_P1(N) and T_P2(N), even when P1 and P2 are from different languages. This margin of error will also overshadow the difference in time it takes to execute a primitive instruction on a computer equipped with a 200 GHz processor versus an antique computer equipped with an 8 MHz processor.

One might argue that such a large margin of error renders our complexity estimates useless. On the other hand, by marginalizing the importance of the choice of language or the speed of the underlying computer, we can feel confident that differences in efficiency between two algorithms that implement the same function are truly due to the choice of algorithm rather than the choice of language or computer.

Measuring the complexity of functions

We can extend our complexity measures for algorithms to complexity measures for functions. For example:

T_F(N) = T_A(N) where A is an optimal implementation of F

It is often quite difficult to compute T_F(N) because this involves not only computing T_A(N), but also proving that A is an optimal implementation of F.

Measuring the size of an input

For functions that operate on integers, the size of the input will be the input itself. For sequences and sets, we take the size of the input to be the length or cardinality of the input.

Example

Assume the function F is defined as the sum of all integers from 0 to N, where N is any non-negative integer:

F(N) = 0 + 1 + 2 + 3 + ... + N

Here are the encodings of three algorithms that implement F:

// recursive algorithm:
int P1(int N) {
if (N <= 0) return 0;
return N + P1(N – 1);
}

// iterative algorithm:
int P2(int N) {
int result = 0;
for(int i = 1; i <= N; i++) {
result = result + i;
}
return result;
}

// Gauss's algoruthm:
int P3(int N) {
return N * (N + 1) / 2;
}

Here are the respective complexity measures:

T_P1(N) = 2 + T_P1(N - 1) = 2 + 2 + T_P1(N - 2) = ... = 2N
t_P1(N) = T_P1(N) = 2N
S_P1(N) = 1 + S_P1(N - 1) = N
s_P1(N) = S_P1(N) = N

T_P2(N) = 2 N
t_P2(N) = T_P2(N) = 2N
S_P2(N) = 2 = # of variables used
s_P2(N) = 2

T_P3(N) = 3
t_P3(N) = 3
S_P3(N) = 0
s_P3(N) = 0

Example

MaxSumTest.java

Comparing growth rates

Notice that the measure of complexity of a program, algorithm, or function turns out to be a function. Usually a measurement is something that can be compared to other measurements, like seconds, miles, dollars, or tons. How do we compare functions? For example, assume A and B are both algorithms that implement function F. To say that A is a more efficient algorithm than A, we need to be able to say that t_A(N) is smaller than t_B(N). But for some values of N t_A(N) may be bigger than t_B(N), while for other values the reverse will be true. Instead, what we try to claim is that t_A is eventually smaller than t_B. In other words, for some positive c and k:

t_A(N) < c * t_B(N) for all N > k

For example, assume:

t_A(N) = 500N
t_B(N) = N²

Then for k = 500

t_A(N) < t_B(N) for all N > k

Computer Scientists abbreviate the above assertion by writing:

t_A = O(t_B)

Or equivalently:

t_B = Ω(t_A)

We also say that t_B majorizes t_A.

If

t_A = O(t_B) && t_B = O(t_A)

we write:

t_A = Θ(t_B)

Of course this is a symmetric relationship:

t_B = Θ(t_A)

If

t_A = O(t_B) && t_B ≠ O(t_A)

we write:

t_A = o(t_B)

Of course we only use t_A and t_B as examples. We could have just as easily used T_A and T_B, S_A and S_B, s_A and s_B, or arbitrary functions F and G for that matter.

Facts about O

Notice that the relationship f = O(g) is not a total ordering. There are many examples of functions f and g such that neither f = O(g) nor g = O(f) are true.

Limit Formulations:

It's not difficult to prove:

f = o(g) iff lim_N->¥f(N)/g(N) = 0
f = o(g) iff lim_N->¥g(N)/f(N) = ¥
f = Θ(g) iff 0 < lim_N->¥f(N)/g(N) < ¥

Using L'Hopital's Rule

Recall:

lim_N->¥f(N)/g(N) = lim_N->¥f'(N)/g'(N)

Fact: Assume f(N) is a degree n polynomial and g(N) is a degree m polynomial, then:

f = o(g) if n < m
g = o(f) if m < n
f = Θ(g) if m = n

Fact: Assume f(N) = log^k(N) (= log base 2 of N raised to the k^th power for k > 0), then

f = o(N)

Fact: Assume f(N) = c^N for c any number > 1, assume g(N) is any polynomial, then:

g = o(f)

Fact: Assume f(N) = g(N) + h(N), and g = O(h), then f = O(h).

Fact: Assume f(N) = g(N) * h(N), then f = O(g * h).

Famous complexity classes

Instead of computing T_A(N) exactly (or any of the other complexity measures), we will often show:

T_A = O(F)

where F(N) is some well known function such as 1 (the constant function), log(N), N, N², N³, or 2^N.

It's worth mentioning a few famous complexity classes:

P = all algorithms A such that T_A(N) = O(N^k) for some k.
PSPACE = all algorithms A such that S_A(N) = O(N^k) for some k.
NP =

union of O(N^k) for all k

The Tyranny of growth rate

Assume function F can be implemented by four algorithms: A1, A2, A3, A4 where:

A1 = Θ(log N)
A2 = Θ(N)
A3 = Θ(N²)
A4 = Θ(2^N)

The following table shows worst case runtimes for these algorithms assuming one operation per millisecond (1 ms = 1/1000 seconds).

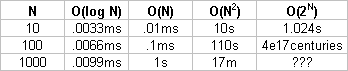
Key:

s = seconds
m = minutes

Notice the runtimes of all three algorithms are reasonable when N is small.