Binary Trees
(Code adapted from Weiss's book.)
Trees
A graph (or network) is a set of nodes and links. A link connects two nodes. A node contains a data element and a set of links to neighboring nodes.
A tree is a special graph in which links connect parent nodes to child nodes. Every node has at most one parent. A node with no children is called a leaf node.
Sorted Sets
Recall that a set is a collection that forbids duplicate elements.
Recall that a sorted set is a set of comparable elements ordered by the logical ordering of the elements.
Recall that AbstractCollection is a partial implementation of the Collection interface. AbstractSet extends AbstractCollection by providing implementations of the removeAll, equals and hashCode methods.
Simple Sorted Sets
public interface SimpleSortedSet {
public Comparable first();
public Comparable last() ;
boolean isEmpty();
int size();
boolean contains( Comparable x );
boolean add(Comparable x)
throws UnsupportedOperationException;
boolean remove( Comparable x )
throws
UnsupportedOperationException;
void clear() throws
UnsupportedOperationException;
}
Overview
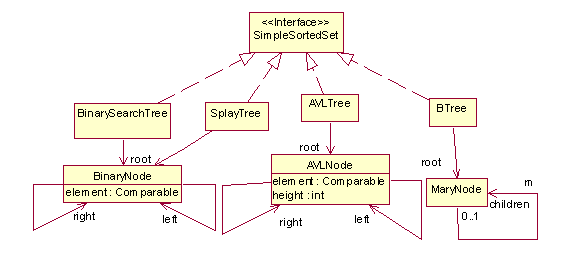
Binary Search Trees
A Binary Search Tree (BST) is a tree satisfying the following properties:
Every node N has at most two children (called N.left and N.right)
Data elements stored by nodes are comparable.
N.left.element < N.element < N.right.element
Binary Nodes
class BinaryNode {
Comparable element;
BinaryNode left;
BinaryNode right;
BinaryNode( Comparable theElement ) {
this( theElement, null, null );
}
BinaryNode(Comparable theElement,
BinaryNode lt, BinaryNode rt) {
element = theElement;
left = lt;
right = rt;
}
}
Binary Search Tree
public class BinarySearchTree implements SimpleSortedSet {
private BinaryNode root = null;
public Comparable first() {
return findMin(root).element;
}
public Comparable last() {
return findMax(root).element;
}
public boolean contains(Comparable x)
{
return find(x, root) != null;
}
public void clear() { root = null; }
public boolean isEmpty( ) { return
size() == 0; }
public int size() { return
size(root); }
public String toString() {
return "{" +
toString(root) + " }";
}
public boolean add(Comparable x) {
BinaryNode node = insert(x, root);
if (node == null) return false;
root = node;
return true;
}
public boolean remove(Comparable x) {
if (!contains(x)) return false;
BinaryNode node = remove( x, root );
if (node == null) return false; // x
not in this
root = node;
return true;
}
//private helper methods:
// recursive version:
private BinaryNode findMin( BinaryNode
t ) {
if( t == null || t.left == null)
return t;
return findMin( t.left );
}
// iterative version:
private BinaryNode findMax( BinaryNode
t ) {
while( t != null && t.right
!= null ) t = t.right;
return t;
}
private int size(BinaryNode t) {
if (t == null) return 0;
return 1 + size(t.left) +
size(t.right);
}
private String toString( BinaryNode t )
{
String result = "";
if( t != null ) {
result += toString( t.left );
result += " " +
t.element;
result += toString( t.right );
}
return result;
}
private BinaryNode find( Comparable x,
BinaryNode t ) {
if( t == null ) return null;
if( x.compareTo( t.element ) < 0
) return find( x, t.left );
if( x.compareTo( t.element ) > 0
) return find( x, t.right );
return t; // Match
}
private BinaryNode insert( Comparable
x, BinaryNode t ) {
if(
t == null ) return new BinaryNode(x);
if( x.compareTo( t.element
) < 0 ) {
t.left = insert( x, t.left );
return t;
}
if( x.compareTo( t.element ) >
0 ) {
t.right = insert( x, t.right );
return t;
}
return null; // x already
in t
}
private BinaryNode remove( Comparable
x, BinaryNode t ) {
if( t == null ) return t; // Item not found; do nothing
if( x.compareTo( t.element ) < 0
)
t.left = remove( x, t.left );
else if( x.compareTo( t.element )
> 0 )
t.right = remove( x, t.right );
else if( t.left != null &&
t.right != null ) { // two children
t.element = findMin( t.right
).element;
t.right = remove( t.element,
t.right );
}
else // return t's only child or
null
t = ( t.left != null ) ? t.left :
t.right;
return t;
}
// Test program
public static void main(
String [ ] args ) {
SimpleSortedSet t = new
BinarySearchTree( );
t.add("One");
t.add("Two");
t.add("Three");
t.add("Four");
t.add("Five");
t.add("Six");
t.add("Seven");
t.add("Eight");
t.add("Nine");
t.add("Ten");
System.out.println(t);
t.remove("Ten");
System.out.println(t);
System.out.println(t.contains("Ten"));
System.out.println(t.contains("One"));
}
}
Program Output
{ Eight Five Four Nine
One Seven Six Ten Three Two }
{ Eight Five Four Nine One Seven Six Three Two }
false
true
Analysis
Let N be a BinaryNode:
height(null) = 0
height(N) = 1 + max(height(N.left), height(N.right))
size(null) = 0
size(N) = 1 + size(N.left) + size(N.right)
Let T be a BinarySearchTree:
height(T) = height(T.root)
size(T) = size(T.root)
Theorem
Assume N is a BinaryNode, then:
size(N) <= 2height(N) - 1
Proof
The proof is by induction on the height of a node.
Base case:
size(null) = 0 <= 2height(null) - 1 = 20 - 1 = 0
Assume:
size(N.left) <= 2height(N.left) - 1
size(N.right) <= 2height(N.right) - 1
Hence:
size(N)
= 1 + size(N.left) + size(N.right)
<= 1 + 2height(N.left) - 1 + 2height(N.right)
- 1
<= 1 + 2height(N)- 2
= 2height(N) - 1
Corollary:
log(size(N) + 1) <= height(N)
A BST is balanced if for every node N:
height(N.left) = height(N.right)
In this case we have equality:
size(T) = 2height(T) - 1
or equivalently
log(size(N) + 1) = height(N)
Most of the BST methods involve searching a branch of a BST, hence most methods are O(log N).
AVL Trees
An AVL tree is a Binary Search Tree satisfying the additional requirement:
|height(T.left) - height(T.right)| < 2
In other words, nodes in an AVL tree are almost balanced.
AVL Nodes
class AVLNode {
Comparable element;
AVLNode left;
AVLNode right;
int height;
AVLNode( Comparable theElement ) {
this( theElement, null, null );
}
AVLNode( Comparable theElement, AVLNode
lt, AVLNode rt ) {
element = theElement;
left = lt;
right = rt;
height = 0;
}
}
AVL Trees
public class AVLTree implements SimpleSortedSet {
private AVLNode root;
public Comparable first() {
return findMin(root).element;
}
public Comparable last() {
return findMax(root).element;
}
public boolean contains(Comparable
x) {
return find(x, root) != null;
}
public void clear() { root = null; }
public boolean isEmpty( ) { return
size() == 0; }
public int size() { return
size(root); }
public String toString() {
return "{" +
toString(root) + " }";
}
public boolean add( Comparable x ) {
AVLNode node = insert(x, root);
if (node == null) return false;
root = node;
return true;
}
public boolean remove( Comparable x )
throws UnsupportedOperationException
{
throw new
UnsupportedOperationException();
}
// private helper methods
/*
Most are the same as the private helper methods in BinarySearchTree except they
operate on AVLNodes instead of BinaryNodes. For example:
*/
private AVLNode find(
Comparable x, AVLNode t ) {
if( t == null ) return null;
if( x.compareTo( t.element ) < 0
) return find( x, t.left );
if( x.compareTo( t.element ) > 0
) return find( x, t.right );
return t; // Match
}
/*
Here's a little utility for computing the height of an AVLNode or null:
*/
private static int
height( AVLNode t ) {
return t == null ? -1 : t.height;
}
// self adjusting insertion:
private AVLNode insert(
Comparable x, AVLNode t ) {
if( t == null ) return new
AVLNode(x);
if( x.compareTo( t.element ) < 0
) {
t.left = insert( x, t.left );
if( height( t.left ) - height(
t.right ) == 2 )
if( x.compareTo(
t.left.element ) < 0 )
t = rotateWithLeftChild( t
);
else
t = doubleWithLeftChild( t
);
} else if( x.compareTo( t.element )
> 0 ) {
t.right = insert( x, t.right );
if( height( t.right ) - height(
t.left ) == 2 )
if( x.compareTo(
t.right.element ) > 0 )
t = rotateWithRightChild( t
);
else
t = doubleWithRightChild( t
);
} else
return null; // x already in t
t.height = Math.max( height( t.left
), height( t.right ) ) + 1;
return t;
}
// Rotations
/**
Rotate binary tree node with left child. For AVL trees, this is a single
rotation for case 1. Update heights, then return new root.|
*/
private static AVLNode
rotateWithLeftChild( AVLNode k2 ) {
AVLNode k1 = k2.left;
k2.left = k1.right;
k1.right = k2;
k2.height =
Math.max( height( k2.left ),
height( k2.right ) ) + 1;
k1.height = Math.max( height(
k1.left ), k2.height ) + 1;
return k1;
}
/**
Rotate binary tree node with right child. For AVL trees, this is a single
rotation for case 4. Update heights, then return new root. It is similar to the
last method.
*/
private static AVLNode
rotateWithRightChild( AVLNode k1 ) {
???
}
/**
Double rotate binary tree node: first
left child with its right child; then
node k3 with new left child. For AVL trees, this is a double rotation for case
2. Update heights, then return new
root.
*/
private static AVLNode
doubleWithLeftChild( AVLNode k3 ) {
k3.left = rotateWithRightChild(
k3.left );
return rotateWithLeftChild( k3 );
}
/**
Double rotate binary tree node: first right child with its left child; then
node k1 with new right child. For AVL
trees, this is a double rotation for case 3. Update heights, then return new
root. It is similar to the last method.
*/
private static AVLNode
doubleWithRightChild( AVLNode k1 ) {
???
}
// Test program
public static void main(
String [ ] args ) {
SimpleSortedSet t = new AVLTree( );
t.add("One");
t.add("Two");
t.add("Three");
t.add("Four");
t.add("Five");
t.add("Six");
t.add("Seven");
t.add("Eight");
t.add("Nine");
t.add("Ten");
System.out.println(t);
System.out.println(t.contains("Ten"));
System.out.println(t.contains("Eleven"));
}
}
Program Output
{ Eight Five Four Nine One Seven Six Ten Three Two }
true
false
Splay Trees
A splay tree is a binary search tree, i.e., a tree of ordinary binary nodes. However, each time a node is accessed by the contains() method, the accessed node is percolated up to the root of the tree through a sequence of rotations.
public class SplayTree implements SimpleSortedSet {
private BinaryNode root = null;
public Comparable first() {
return findMin(root).element;
}
public Comparable last() {
return findMax(root).element;
}
public boolean contains(Comparable x)
{
return find(x, root) != null;
}
public void clear() { root = null; }
public boolean isEmpty( ) { return
size() == 0; }
public int size() { return
size(root); }
public String toString() {
return "{" +
toString(root) + " }";
}
public boolean add(Comparable x) {
BinaryNode node = insert(x, root);
if (node == null) return false;
root = node;
return true;
}
public boolean remove(Comparable x) {
if (!contains(x)) return false;
BinaryNode node = remove( x, root );
if (node == null) return false; // x
not in this
root = node;
return true;
}
// etc.
}
private BinaryNode find(Comparable x, BinaryNode x) {
locate node with element = x in the
usual way.
percolate this node to the root using
rotations
}
B-Trees
A B-tree is a tree of M-ary nodes:
class Node {
}
class parentNode extends Node {
<= M Node children
}
class LeafNode extends Node {
// <= L Comparable children
}
class MAryNode {
Comparable min; // smallest element
Comparable[] leafChildren;
MAryNode[] parentChildren;
int order; // = max children
boolean leaf;
MAryNode(int m, boolean leaf) {
children = new Comparable[m];
order = m;
this.leaf = leaf;
}
}
Such that:
1. Between L/2 and L elements are stored in leaf nodes
2. All leaf nodes are at the same depth
3. Parent nodes have between M/2 and M children
4. The root node has between 2 and M children
class BTree implements SimpleSortedSet {
private MAryNode root;
BTree(int m) {
root = new MAryNode(m, false);
}
boolean isEmpty() { return size() == 0;
}
int size() { /* exercise */ }
boolean contains( Comparable x ) {
}
boolean add(Comparable x) {
// the usual algorithm
}
boolean remove( Comparable x ) {
// exercise
}
void clear() {
for(int i = 0; i < root.order;
i++) {
root.children[i]
= null;
}
}
}
Assume T is an order m B-tree. Assume T.size() = N. Then the longest path is T is logM(N)
Problems
Problem 1
Implement the SortedSet interface from the Java Collections Framework as an AVL tree:
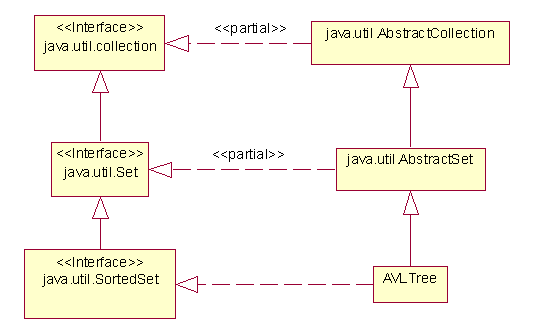
You may assume that removing elements is not allowed.
Hint: The hard part of this problem is implementing the iterator method. Here is how I would start (just a sketch):
class AVLTree extends AbstractSet implements SortedSet {
private AVLNode root;
private Comparator comparator = null;
public AVLTree() {
root = null;
comparator = null;
}
public AVLTree(Comparator c) {
root = null;
comparator = c;
}
public AVLTree(Collection elems) {
root = result of inserting all
elems;
comparator = null;
}
public AVLTree(Collection elems,
Comparator c) {
root = result of inserting all
elems;
comparator = c;
}
private void CompareTo(Object elem1,
Object elem2) {
if (comparator != null)
return
comparator.compareTo(elem1, elem2);
return (Comparable)elem1.compareTo((Comparable)elem2);
}
public Iterator iterator() {
return new
AVLIterator(findMin(root));
}
class AVLIterator implements Iterator {
private AVLNode next; // next unseen
node
private AVLNode last; // last node
seen
public AVLIterator(AVLNode first) {
next = first;
last = null;
}
public boolean hasNext() throws
ConcurrentModificationException {
return (next != null);
}
public Object next() throws
NoSuchElementException,
ConcurrentModificationException {
???
}
public void remove() throws
IllegalStateException,
UnsupportedOperationException,
ConcurrentModificationException {
throw new
UnsupportedOperationException();
}
// etc.
}
// etc.
}
The hard part is next(), which sets last to next and next to the node containing the least element greater than last:
public Object next()
throws
NoSuchElementException,
ConcurrentModificationException {
last = next;
next = leastGreater(last);
return last.element;
}
If last has a right child, then this is simply findMin(last.right).
private AVLNode leastGreater(AVLNode node) {
if (node.right != null) return
findMin(node.right);
???
}
If last has no right child, then this is findMin(node.right) where node is the ancestor of last having the least element greater than last:
private AVLNode leastGreater(AVLNode node) {
if (node.right != null) return
findMin(node.right);
Node ancestor = root;
Node leastGreaterAncestor = null;
while(ancestor != node) {
if (node < ancestor <
leastGreaterAncestor)
leastGreaterAncestor = ancestor;
ancestor = ancestor.left or
ancestor.right
}
return leastGreaterAncestor;
}
Problem 2
A diary consists of a set of daily entries. An entry has the form:
class Entry implements Comparable {
String text;
Date date;
// etc.
}
Implement and test a diary using your AVL implementation of sorted sets:
class Diary {
private SortedSet entries = new
AVLTree();
public void addEntry(String text) { ???
}
public String toString() {
iterator p = entries.iterator();
while(p.hasNext()) {
// pretty print date and text of
p.next();
}
}
public static void main(String[] args)
{
// create and print a juicy diary
}
}
Problem 3
Create a program that reads a text file one line at a time (use a BufferedReader for this) and generates a line number index.
It scans each line for tokens bracketed by asterisks (use StringTokenizer for this). For example:
*life and liberty*
The index itself is a Map in which keys are Strings and associated values are sets of line numbers. When the indexer encounters an index entry, it either makes a new entry in the map, or it adds the line number to the set indexed by the entry.
Read over the section of character streams in
http://www.mathcs.sjsu.edu/faculty/pearce/java2/jpop/chp5/chp5.htm