Programming with Objects
Narrowing the Semantic Gap
The real world context of an application is called the application domain. For example, the application domain of a warehouse inventory program is the warehouse itself, including the associated tangibles (forklifts, pallets, goods, etc.), transactions (receiving goods, receiving purchase orders, locating goods, shipping goods, sending invoices, receiving payments, taking inventory), places (loading docks, receiving docks, bins, aisles, etc.), and people (customers, managers, truckers, suppliers, workers).
Taken together, the artifacts produced by a programmer (documentation, files, modules, code, test results, tools, computers, etc.) form the solution domain. We can partition the solution domain into levels. Abstract, high-level design documents (diagrams, data dictionaries, requirement specifications, models, etc.) belong to the upper levels of the solution domain, while more specific, detailed artifacts (data structures, statements, function definitions, type definitions, hardware, etc.) belong to the lower levels.
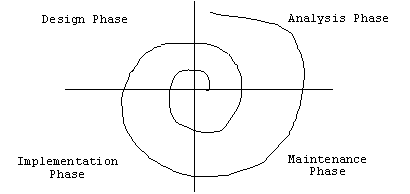
Developing an application can be loosely divided into four phases:
1. Analysis Phase: Understand and specify the application's requirements by building a model of the application domain.
2 a. Early Design Phase: Use the application domain model to develop a model of the application itself (i.e., the application's architecture or design). The architecture should describe the major components and their relationships.
2 b. Late Design Phase: Repeatedly refine the architecture, specifying details about the components, components of the components, etc.
3. Implementation Phase: When the architecture reaches a sufficient level of detail, turn the design into source code.
4. Maintenance Phase: This phase includes configuring, debugging, testing, and improving the application.
Of course programmers often pass through these phases more than once:

We can summarize all but the last phase with a diagram:
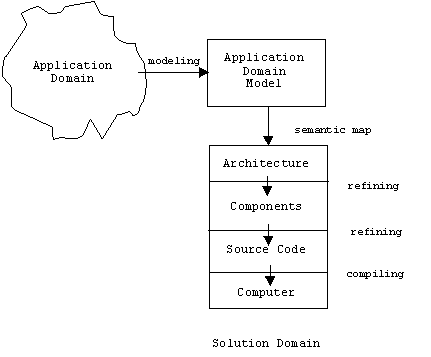
Building a good model of the application domain is nearly impossible, unless you happen to be a programmer and a domain expert (e.g., the warehouse manager). We'll ignore this little paradox for now. If you do end up with a reasonable model of the application domain, another nasty problem arises.
Recall the modularity principle:
Programs should be constructed out of coherent, loosely coupled modules.
The basic module of procedural programming is the function. Following the top down design method, we specify the high level architecture of our application in terms of the principle functions and data structures. We refine the architecture by identifying and defining supporting functions. We repeat this refinement process until there are no more undefined supporting functions.
The problem is that the objects in the application domain (transactions, places, people, tangibles, etc.) don't much resemble the items in the solution domain (functions and data structures). Therefore, the model of the application domain will be quite different from the model of the application. How will we use the model to derive the architecture? It seems that the semantic map must bridge a very wide gap between two very different worlds. This gap is called the semantic gap.
Object Oriented Programming
A paradigm is a collection of tools, components, and techniques used to build models. We can restate the basic problem in terms of paradigms: We use the object paradigm to model application domains: identify and describe the important objects and their relationships, but we use the procedural paradigm to model programs: identify and describe the important functions and data structures.
Why do we use different paradigms? We use the object paradigm to model the application domain because the application domain consists of objects. We use the procedural paradigm to describe solutions because each level of the solution domain is an abstraction of the level below it. The bottom level is the computer itself, which is composed of interconnected memory modules (data structures) and processors (functions). Regardless of the structure of the application domain, our high level architecture must ultimately be mapped to the architecture of the underlying computer.
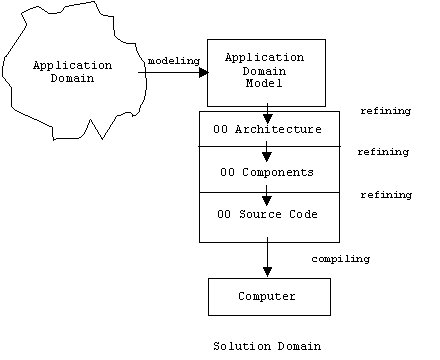
The basic program building blocks of object oriented programming languages like Smalltalk and Java are objects, not functions and data. Like its application domain counterpart, the behavior of a solution domain object depends on its internal state, the environment, and stimuli from other objects. Object-oriented design and programming (i.e., designing and programming with objects) narrows the semantic gap because we can represent application domain objects by corresponding solution domain objects. Mapping the application domain model to the application's architecture is only a matter of model refinement. The semantic gap is displaced. It is now between the source code and the computer, safely hidden by the compiler:
Objects
C++ supports procedural programming and object-oriented programming (a recipe for disaster). A C++ object encapsulates services (behavior) and attributes (state). Objects are software analogs of integrated circuits (sometimes objects are called software ICs). Objects, not functions and data, are the fundamental building blocks of object oriented programs.
The basic interaction between two objects fits a client-server model. The client object requests a service from the server object. The server object may respond with a result:
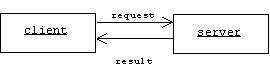
Of course the server and client can change roles. Different object oriented systems have different ways of requesting services. Some systems view requests and results as messages sent between the client and the server (the Win32 API, for example). In C++ attributes are encapsulated variables called member variables, services are encapsulated functions called methods or member functions, a service request-- also called a method invocation-- is a call to a member function, and the result is the corresponding return value.
Here's some sample C++ client code. The two bank account objects can be regarded as servers. In this example the client (not shown) might represent a bank:
Account a; // create an account
a.deposit(50); // invoke a's deposit method to add $50
cout << '$' << a.getBalance() << '\n'; // prints $50
Account *b = new Account(); // create an account
b->deposit(30); // invoke *b's deposit service to add $30
b->withdraw(20); // invoke *b's withdraw service to take $20
cout << '$' << b->getBalance() << '\n'; // prints $10
The attribute of a bank account is its balance. The services provided by bank accounts are the member functions getBalance(), withdraw(), and deposit(). Note that calls to the member functions must be qualified with the name of the server object using the dot or arrow operator.
Classes
A class is a pattern for constructing objects. An object constructed by a class is called an instance of that class. All instances of a class provide the same services and attribute variables but differ in the values stored in these variables.
In C++ the declaration of a class may include member functions, and member variables:
// Account.h
class Account
{
public:
// member functions
double getBalance();
void deposit(double amt);
void withdraw(double amt);
private:
// member variable
double balance;
};
From this definition it might appear that there is only a single variable called balance. This isn't true. Each bank account instance will encapsulate a variable called balance. For example, the earlier declarations of a and b created two variables called balance:
a.balance
b->balance
Each object could also encapsulate the member functions, but this would be wasteful. Instead, there is only one withdraw() function for all bank account objects. Officially, this function is called:
Account::withdraw()
C++ can determine which account money is being withdrawn from by the account instance that qualifies each call to withdraw():
a.withdraw(20); // withdraw $20 from a
b->withdraw(1); // withdraw $10 from *b
Classes vs. C Structs
The syntax of a class declaration is similar to the syntax of a struct declaration. In fact, we can replace the reserved word "class" by the reserved word "struct" in the definition above without any affect. (Officially, structs, unions, and classes are all called classes.) However, there are some striking differences between class declarations and traditional C struct declarations.
Scope Control
The scope of a declaration is the region of the program where the binding created by the declaration is visible. For example, global declarations have global scopes. They are visible throughout the entire program. Local declarations have local scopes. They are only visible inside the block they are declared in. The member variables grouped by a C structure have the same scope as the structure. In the following example:
struct Date
{
int day, month, year;
} today;
today is a Date variable that groups three integer member variables: today.day, today.month, and today.year. The member variables are visible anywhere the today variable is visible. If today is a global variable, then so are the member variables.
C++ programmers can control the scopes of their class members (i.e. member variables and functions). There are three scopes: public, private, and protected. The scope of a member is determined by the section of the class declaration it is declared in. In the Account example balance is private because it is declared in the private section. The constructor and member functions are all public because they are declared in the public section. There is no protected section in this declaration. A class can have multiple public, protected, and private sections. Members not declared in a section are assumed to be private in class declarations and public in struct declarations.
Members with public scope have the same scope as the object that encapsulates them. They are visible to the clients of the encapsulating object. Members with private scope are only visible to other members. For example, a global function can call the constructor and methods of a global account variable, but not its balance variable:
int main()
{
Account a(100); // legal
a.getBalance(); // legal
a.deposit(100); // legal
a.withdraw(20); // legal
a.balance; // error!
}
Why do we need three scopes? We need at least two scopes: public and private. The public members define the public interface of the class. They are accessible to all clients of the class. The private members are only accessible by other members. They support the implementation of the public members.
C++ recognizes two types of clients: end users and value adders. Value adders are interested in modifying or adding features to a class for use by their clients. Although value adders still can't access the private members of a class, the class can make certain additional supporting members available to them that are not available to end users. These are the members with protected scope.
Member Functions
The first thing that catches the eye is the occurrence of function prototypes for deposit(), withdraw(), and getBalance() inside the Account class declaration. These are the member functions. The implementations of the member functions are normally placed in another file, see below. By contrast, a struct in C is only a mechanism for grouping related variables, not variables and functions. The function prototypes can be regarded as specifying the interface each instance of the Account class implements.
In C there is only one type of function: global functions. C++ has global functions, too, but member functions are different from global functions in some significant ways, so it will be important for us to distinguish between member functions and global functions.
The implementations of the constructors and member functions can be separated from their interfaces in C++. Outside of its class declaration a member function must be qualified by its class name to remind the C++ compiler where it came from. Unfortunately, qualifying a member function definition uses different syntax from qualifying a member function call. Assume aaa is an instance of a class AAA that has a member function called fun(). We use the dot operator to qualify the call to fun(), but we use the scope resolution operator(::) to qualify the definition of fun():
aaa.fun(); // calling fun()
void AAA::fun() { ... } // defining fun()
Here are the implementations of the Account member functions:
// Account.cpp
#include "Account.h"
#include <iostream>
using namespace std;
Account::Account(double amt) { balance = amt; }
double Account::getBalance() { return balance; }
void Account::deposit(double amt) { balance += amt; }
void Account::withdraw(double amt)
{
if (amt <= balance)
balance -= amt;
else
cout << "sorry, insufficient funds\n";
}
Constructors
An important principle in C++ is that objects should be initialized at the time they are created. If creation and initialization are separated, then there is a risk that the programmer will forget to perform the initialization or that some client will try to use the object before it is initialized.
When an object is created, for example in a declaration:
Account z;
C++ automatically calls a constructor function that initializes the object's member variables. If no constructor is declared, then C++ automatically generates two constructors. The default constructor assigns random values to the object's member variables, and the copy constructor assigns the member variables of a specified object to the corresponding member variables of the object being created. For example, assume two bank accounts are created and their balances displayed:
Account a, b(a);
cout << "a.balance = " << a.getBalance() << '\n';
cout << "b.balance = " << b.getBalance() << '\n';
Here is what gets printed on my computer:
a.balance = 2.64203e-308
b.balance = 2.64203e-308
Note that b.balance has the same value as a.balance, almost 0, but if interest is compounded monthly, then this could add up to a few cents over a couple hundred billion years! In effect, b is a clone of a. Of course they are different objects. Depositing money in one account has no effect on the other:
a.deposit(50);
b.deposit(30);
cout << a.getBalance() << '\n'; // prints 50
cout << b.getBalance() << '\n'; // prints 30
Relying on compiler-generated constructors is a bad idea, so C++ allows programmers to define their own constructors. The name of a constructor always matches the name of the class (since the primary service of the class is to construct instances), and the constructor does not have a return type. Overloading permits multiple constructors as long as their parameter lists are different.
class Account
{
public:
// constructors
Account(double amt = 0);
// member functions
double getBalance();
void deposit(double amt);
void withdraw(double amt);
private:
// member variable
double balance;
};
Here is the implementation of the constructor:
Account::Account(double amt /* = 0 */) { balance = amt; }
If a programmer defines any constructor at all, then the compiler will not generate a default constructor. Therefore, if a programmer defines a constructor, he should also define a default constructor (i.e. a parameterless constructor). In some situations, for example declaring an array of objects:
Account accounts[50]; // error if no default constructor exists
the default constructor is used to initialize the array components.
By specifying a default argument (0) for the Account constructor's parameter, my constructor functions as a default constructor and a single parameter constructor.
We can call a constructor directly:
Account(500); // creates an anonymous account with $500
This is necessary if we want to create a new object on the heap, as a return value, or as the right side of an assignment statement:
Account *z = new Account(50); // z->balance = $50
Account makeAccount(double bal) { return Account(bal); }
Account y = Account(75); // y.balance = $75
The last example is wasteful. It is equivalent to:
Account y; // Account(0) called
Account temp(75); // Account(75) called
y = temp; // y.balance = temp.balance
More commonly, we can get C++ to call a constructor by using an argument list as a declaration initializer:
Account a(50), b(100), c;
In this example a.balance is initialized to $50, b.balance is initialized to $100, and c.balance is initialized to $0.
You might think the declaration:
Account c();
initializes Account c by calling the Account::Account() constructor with its default argument, 0. Although this interpretation makes sense, this syntax is already used by C (hence inherited by C++) to declare a parameterless function c that returns an instance of the Account class. Instead:
Account c;
declares an Account variable c initialized using the default argument.
Copying Objects
Assigning one object to another creates a copy of the first object. For example, if a and *b are bank accounts, then:
*b = a;
copies the a.balance into b->balance.
Copies of objects are made in other places, too. global function with an account value parameter or that returns an account creates account copies. Assume:
Account clone(Account x)
{
return Account(x.getBalance() + 50);
}
Calling *b = clone(a) copies a to x. The copy constructor generated by the compiler is used to make this copy. Next an anonymous temporary account is made from x.balance + 50. Finally, this temporary is copied into *b.
Inline Member Functions
Programmers can put implementations of some or all member functions, constructors, etc. inside class declarations:
// from Account.h
class Account
{
public:
// constructor
Account(double amt = 0) { balance = amt; }
// member functions
double getBalance() { return balance; }
void deposit(double amt) { balance += amt; }
void withdraw(double amt);
private:
// member variable
double balance;
};
Implementing a member function inside a class declaration makes it an inline function, so programmers should heed the usual warnings about overly complex inline functions when following this practice.
The Implicit Parameter
The implementation of getBalance() refers to balance without qualifying which account it belongs to. How does it know which balance to return? Of course the intended account qualifies the call to getBalance():
a.getBalance(); // returns a.balance
b->getBalance(); // returns b->balance
But how does the C++ compiler know how to translate the balance that appears in getBalance() into a specific address? Although invisible, getBalance() really has a parameter of type Account*, which qualifies balance. Here's how getBalance() might look in C with its implicit parameter revealed:
double getBalance(Account *this) { return this->balance; }
The method invocation a.getBalance() translates into the C call getBalance(&a).
We can use the implicit parameter as a convenient reference to the encapsulating object. For example, suppose suspiciously large deposits are to be reported to the IRS. The IRS might be represented by a class with a static report() method:
class IRS
{
public:
double SUSPICIOUS = 1000;
void report(Account* a, double amt)
{
// call Janet Reno!
}
// etc.
} irs;
If necessary, Account's deposit() method can pass its encapsulating object to irs.report() using the implicit parameter:
void Account::deposit(double amt)
{
balance += amt;
if (amt >= irs.SUSPICIOUS) irs.report(this, amt);
}
Note: global functions do not have implicit parameters. This only makes sense for member functions.
How can we indicate that the implicit parameter is constant? For example, Account::getBalance() method only returns the balance. It doesn't alter it. To declare that the implicit account parameter is constant, we write const after the parameter list:
class Account
{
public:
Account(double amt = 0) { balance = amt; }
double getBalance() const { return balance; }
void deposit(double amt) { balance += amt; }
void withdraw(double amt);
private:
double balance;
};
Why didn't we write const after deposit() and withdraw()?
Static Members
Suppose we wanted to keep track of the total number of accounts. Where would be the best place to store this number? If it's a global variable, then it could get altered by a rogue function. If we made it a member variable, then every account object would have a copy. Each time the total changed, we would have to change it in each account instance. A third option is to make it a private member of the Account class rather than a member of instances of the class. This is done by writing the reserved word "static" in front of the variable. Functions can be class members, too. This is the case with getTotal().
// from Account.h
class Account
{
public:
// constructors
Account(double amt = 0);
Account(const Account& a); // copy constructor
~Account(); // destructor, see below
// instance member functions
double getBalance();
void deposit(double amt);
void withdraw(double amt);
// class member function
static int getTotal() { return total; }
private:
// instance member variable
double balance;
// class member variable
static int total;
};
Actually, the declaration of total isn't a definition. In other words, it only associates a type to total, not a variable. To remedy this situation, we must define and initialize total. Account.cpp would be a good place to do this:
int Account::total = 0;
Notice that outside of the class declaration, then name of the variable must be qualified with the class name (using the scope resolution operator), not the name of an account object. This makes sense because total is not associated with individual accounts, rather it is associated with the Account class. The same is true for client calls to the getTotal() function:
Account::getTotal();
Of course client's can't access total since it is private.
We can increment the total in the constructor:
Account::Account(double amt /* = 0 */)
{
balance = amt;
total += 1;
}
We must also introduce a copy constructor because the one generated by C++ only copies variables. It doesn't increment total:
Account::Account(const Account& acct)
{
balance = acct.balance;
total += 1;
}
Among other times, the copy constructor is called to copy account arguments into account parameters. For example, assume the following function is defined:
bool rich(Account x) { return x.getBalance() > 100000; }
Assume a is an account:
Account a(50);
When a is passed to rich(), the copy constructor copies a.balance into x.balance and increments total.
Suppose the copy constructor's parameter is a value parameter instead of a reference parameter:
Account::Account(const Account acct)
{
balance = acct.balance;
total += 1;
}
Calling rich(a) calls Account(a), as before, but now a must also be copied into the copy constructor's parameter, acct. The copy constructor is called to make this copy. This turns into a never-ending sequence of calls to Account(a)!
Destructors
C++ allows programmers to make funeral arrangements for their objects by defining destructors. A destructor has the name of the class preceded by "~" and never has parameters. It is automatically called just before an object is deleted from the heap or popped off the stack:
Account::~Account()
{
total -= 1;
}
Initializer Lists
How are constant and reference members initialized? Initializing them in a constructor's block is too late. The compiler doesn't allow us to assign values to constants:
class Demo
{
public:
Demo(double a, double b, double c)
{
x = a; // error, references are constant pointers
y = b; // error, can't assign a constant
z = c; // ok, z is a variable
}
// etc.
private:
double& x;
const double y;
double z;
};
The solution provided by C++ is the initializer list. Initializer lists appear between the header and block of a constructor:
Constructor(...)
: init1, init2, init3
{
etc
}
and alter the (random) default values the compiler uses when it first creates memory for an object.
class Demo
{
public:
Demo(double a, double b, double c)
: x(a), y(b), z(c)
{} // empty block!
// etc.
private:
double& x;
const double y;
double z;
};
For example, suppose we want to turn the tax calculator from a few chapters back into an object. Recall that the tax calculator depended on several constants (rates, income levels, etc.) These must now be defined in the initializer list:
class TaxCalculator
{
public:
TaxCalculator(double inc = 0,
double rate1 = .3,
double rate2 = .2,
double rate3 = .1,
double inc1 = 50000,
double inc2 = 20000,
double inc3 = 5000)
:maxRate(rate1),
medRate(rate2),
minRate(rate3),
maxMedIncome(inc1),
maxMinIncome(inc2),
maxLowIncome(inc3),
maxMinTax(minRate * (maxMinIncome - maxLowIncome)),
maxMedTax(medRate *
(maxMedIncome - maxMinIncome) + maxMinTax)
{
income = inc;
calc(); // tax = ...
}
double getIncome() { return income; }
void setIncome(double inc) { income = inc; calc(); }
double getTax() { return tax; }
ostream& print(ostream& os = cout);
private:
void calc();
const double maxRate;
const double medRate;
const double minRate;
const double maxMedIncome;
const double maxMinIncome;
const double maxLowIncome;
const double maxMinTax; // tax on $20000
const double maxMedTax; // tax on $50000
double income, tax;
};
Tax calculation uses a multi way conditional to compute a progressive tax:
void TaxCalculator::calc()
{
if (maxMedIncome < income)
tax = maxRate * (income - maxMedIncome) + maxMedTax;
else if (maxMinIncome < income)
tax = medRate * (income - maxMinIncome) + maxMinTax;
else if (maxLowIncome < income)
tax = minRate * (income - maxLowIncome);
else if (0 <= income)
tax = 0;
else
cerr << "Error: income must be non-negative\n";
}
This is simply a printing utility:
ostream& TaxCalculator::print(ostream& os = cout)
{
os << "Tax on $" << income << " = $" << tax << '\n';
return os;
}
The initializer list is also a good place to initialize member objects. For example, assume temperatures are represented as objects:
class Temperature
{
public:
Temperature(double deg = 0) { value = deg; }
double getValue() { return value; }
void setValue(double deg) { value = deg; }
// etc.
private:
double value;
};
A thermometer object might contain a temperature object:
class Thermometer
{
public:
Thermometer(double deg = 0, string sc = "Celsius")
{
temp = Temperature(deg);
scale = sc;
}
string getScale() { return scale; }
ostream& print(ostream& os = cout)
{
os << temp.getTemp() << " degrees " + scale << '\n';
return os;
}
private:
Temperature temp;
string scale;
};
Consider the first line of the constructor:
temp = Temperature(deg);
On the right hand side, an anonymous, temporary temperature object is being created an initialized. This object is then copied into temp by the assignment operator:
Temperature t(deg);
temp = t;
This is especially wasteful, because the member variable temp.value, was already initialized to a random value when it was first allocated. Instead of a random value, we can get the runtime memory system to use our temperature constructor by initializing temp in the initialzer list:
class Thermometer
{
public:
Thermometer(double deg = 0, string sc = "Celsius")
: temp(deg)
{
scale = sc;
}
string getScale() { return scale; }
ostream& print(ostream& os = cout)
{
os << temp.getTemp() << " degrees " + scale << '\n';
return os;
}
private:
Temperature temp;
string scale;
};
Sometimes the compiler doesn't generate assignment operators for a class. This happened for TaxCalculator, although I'm not sure why. When this happens, we must initialize member objects in the initializer list:
class W2Form
{
public:
W2Form(string nm = "?",
string id = "?",
double inc = 0)
:calc(inc)
{
//calc = TaxCalculator(inc); this fails!
name = nm;
ssn = id;
}
ostream& print(ostream& os = cout)
{
os << "Name = " + name + '\n';
os << "ssn = " + ssn + '\n';
os << "income = " << calc.getIncome() << '\n';
os << "tax = " << calc.getTax() << '\n';
return os;
}
private:
string name;
string ssn;
TaxCalculator calc;
};
Friends
We can grant functions and classes access to the private members of a class using the friend declaration. For example, assume an IRS class is defined that provides functions for computing taxes. Also assume a global function is defined for computing fees levied by a bank. We want the member functions of the IRS class and the global function for computing fees to have access to the private balance variable encapsulated by account objects. To do this, simply write the name of the class or function prototype preceded by the reserved word friend, in the Account declaration:
class Account
{
public:
friend class IRS;
friend double computeFee(double amt);
// etc.
private:
double balance;
};
Note that class IRS and computeFee() can't declare themselves friends from outside the class. This would defeat the purpose of having private data. Only the implementer of Account can declare friends.
UML Notation
A class diagram is a blueprint of a program. One notation system for making diagrams is called the Universal Modeling Language (UML). Classes in a UML diagram appear as boxes showing the class name and, optionally, the class attributes and services:

Objects are boxes showing the name and/or class of the object together with the object's current attribute values:
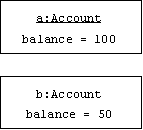
An association is a relationship between objects, although it is drawn as a line connecting classes. The line can show multiplicity, direction, and a label. For example, the following association:
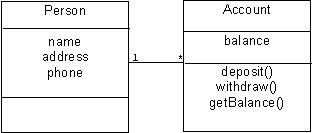
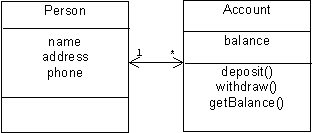
shows one instance of the Person class may be associated with multiple instances of the Account class. In C++ this might mean that an instance of the Person class contains a list of pointers to instances of the Account class. Each instance of the Account class might also have a pointer back to its associated instance of the Person class. We can indicate that it is possible to navigate from instances of one class to instances of another by putting arrow heads on our associations:
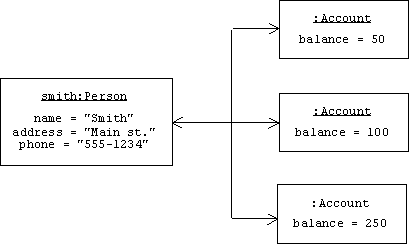
We can show associations in object diagrams, too. In this case the multiplicity shown in the class diagram turns into multiple Account instances and multiple arrows:
Aggregation
A special type of association occurs when instances of one class are containers (stacks, queues, vectors, lists, etc.) and instances of the other class are storables (i.e., the contained items). We call the association between a container class and a storable class aggregation. A special UML link is used to denote aggregation. For example, assume we want to create a stack of accounts. Here is how this is expressed in UML:
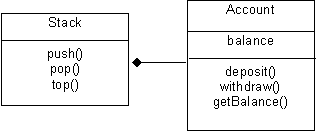
Problems
The Rational Number Stack Calculator
Sample Session
Calc is a console program that allows users to perform stack arithmetic on rational numbers. Here is a sample session. Program output is shown in bold face (user input is in normal font):
C: calc
-> push 3/4
done
-> push 5/6
done
-> push 1/12
done
-> display stack
<3/4, 5/6, 1/12>
-> add
done
-> top
11/12
-> display stack
<11/12, 3/4>
-> mul
done
-> top
33/48
-> pop
done
-> display stack
<>
-> quit
bye
C:
You can deduce from the session that arithmetic commands (including div and sub) replace the top two items on the stack with their arithmetic combination.
Structure
The stack calculator consists of an interpreter object and a stack object containing rational number objects:
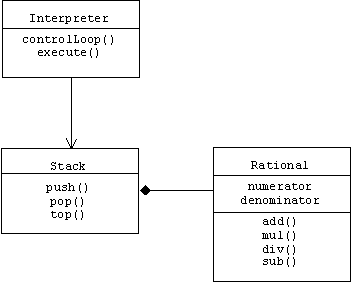
The Interpreter
An interpreter consists of a control loop, a command processor, and a context:
class Interpreter
{
public:
Interpreter(Context* s = 0) { context = c; }
void controlLoop();
string execute(string cmmd);
private:
Context* context;
};
The context of a stack calculator is a stack:
typedef Stack Context;
The control loop follows the model developed earlier, except this time it's a member function. The real work is done by the command processor, execute(), which must inspect the command, call the appropriate execute sequence, then return the result.
Rational Numbers
A rational number (i.e. a fraction) has two integer parts: a numerator and a positive denominator. Rational numbers can be combined arithmetically like any other numbers (see your middle school algebra book to remember how):
class Rational
{
public:
Rational(int n = 0, int d = 1);
Rational add(const Rational& r) const;
Rational mul(const Rational& r ) const;
Rational sub(const Rational& r) const;
Rational div(const Rational& r) const;
int getNumerator() { return num; }
int getDenominator() { return den; }
double toDouble() { return int(num) / int(den); }
ostream& write(ostream& os = cout) const;
istream& read(istream& is = cin);
private:
int num, den;
};
Question: arithmetic operators normally combine two numbers, but the arithmetic operators above only have a single rational number parameter. Where is the other number?
The Rational constructor automatically reduces and normalizes the numerator and denominator. For example:
Rational r(4, -8); // r.num = -1, r.den = 2
Rational q(5, 0); // divide by 0 error
To reduce a rational number replace the numerator and denominator by the result of dividing them by their greatest common divisor:
div = gcd(num, den);
num = num/div;
den = den/div;
Here's an efficient gcd() function you can add to your utils.h file:
int gcd(int n, int m)
{
if (n < 0 || m < 0)
return gcd(abs(n), abs(m));
if (n < m)
return gcd(m, n);
if (m == 0)
return n;
else
return gcd(m, n % m);
}
The Stack
The context of the interpreter commands will be a last-in-first-out store called a stack. The implementation below simply encapsulates an array of items. The stack pointer, sp, equals the index of the next available location in the items array:
Class Stack
{
public:
void push(const Item& i);
Item pop();
Item top() const;
bool isFull() const { return sp == STACK_SIZE; }
bool isEmpty() const { return sp == 0; }
ostream& print(ostream& os = cout) const;
private:
Item items[STACK_SIZE];
int sp = 0;
};
The definitions of STACK_SIZE and Item should be separated from the definition of Stack:
const int STACK_SIZE = 100;
typedef Rational Item;
In this application it might be wise to define a few global functions that perform stack arithmetic:
void add(Stack& s); // replace top two items by sum
void mul(Stack& s); // replace top two items by product
void div(Stack& s); // replace top two items by quotient
void sub(Stack& s); // replace top two items by difference
It wouldn't be a good idea to make these member functions of Stack since some definitions of Item might not support arithmetic operations.
main()
The main function should look like this:
int main()
{
Stack nums;
Interpreter calc(&nums);
calc.controlLoop();
return 0;
}
Problem
Finish and test the stack calculator.
Problem
How would you implement an undo command in your interpreter?
Problem
Replace your implementation of Stack with the standard library implementation of stack:
#include <stack>
using namespace std;
typedef stack<Rational> Stack;
What changes must you make in the rest of your program?
Grids
The Grid class provides poor man's graphics:
class Grid
{
public:
enum { rowSize = 30, colSize = 24 };
Grid() { clear(); }
void plot(int row, int col, char c = '*')
{
grid[row % rowSize][col % colSize] = c; // wrap around
}
ostream& show(ostream& os = cout);
void hPlot(int row, int col, const string& s);
void vPlot(int row, int col, const string& s);
void plotLine(int xstart, int ystart,
int xend, int yend, char c = '*');
void clear(char c = ' ');
int getColSize() { return colSize; }
int getRowSize() { return rowSize; }
char getChar(int row, int col)
{
return grid[row % rowSize][col % colSize];
}
private:
char grid[rowSize][colSize];
};
Here are the implementations of the member functions:
ostream& Grid::show(ostream& os)
{
for(int i = 0; i < rowSize; i++)
{
for(int j = 0; j < colSize; j++)
os << getChar(i, j);
os << '\n';
return os;
}
}
void Grid::clear(char c /* = ' ' */)
{
for(int i = 0; i < rowSize; i++)
for(int j = 0; j < colSize; j++)
grid[i][j] = c;
}
// horizontal plot
void Grid::hPlot(int row, int col, const string& s)
{
for(int i = 0; i < s.size(); i++)
plot(row, col++, s[i]);
}
// vertical plot
void Grid::vPlot(int row, int col, const string& s)
{
for(int i = 0; i < s.size(); i++)
plot(row++, col, s[i]);
}
// Stolen from Horstmann's book.
//(He got it from Foley & Van Dam's book)
void Grid::plotLine(int xstart, int ystart,
int xend, int yend, char c)
{
int dx = xend - xstart; // run
int dy = yend - ystart; // rise
if (abs(dy) < abs(dx)) // |slope| < 1
{
if (dx < 0) // xend < xstart
{
plotLine(xend, yend, xstart, ystart, c);
return;
}
// plot (x, y) for increments of x & y
double y = ystart + 0.5;
double m = double(dy)/double(dx); // = slope
for(int x = xstart; x != xend; x++, y += m)
plot(int(y), x, c);
}
else // 1 <= |slope|
{
if (dy < 0) // yend < ytart
{
plotLine(xend, yend, xstart, ystart, c);
return;
}
// plot (x, y) for increments of x & y
double x = xstart + 0.5;
double m = double(dy)/double(dx); // = slope
for(int y = ystart; y != yend; y++, x += m)
plot(int(y), x, c);
}
plot(yend, xend, c);
}
Turtle Graphics
A turtle is a virtual creature that wanders around a grid marking it with a pen. The turtle's basic attributes are its pen, its position in the grid, its heading, and a flag indicating if its pen is up or down. Clients can set the turtle's heading, move it forward n steps, and change its pen state:
class Turtle
{
public:
Turtle(char p = '*', int r = 0, int c = 0);
void move(int steps = 1);
void turn(Heading h);
void penUp();
void penDown();
private:
bool penState; // true = up
char pen;
int row, col;
Heading dir;
};
A heading is just a compass direction. On the grid, north (N) is the direction of lower row numbers:
enum Heading {N, E, S, W};
Use the interpreter class to implement a turtle graphics program. The basic user commands are: show grid, erase grid, move n, turn right, turn left, pen up, and pen down. A context consists of a grid and a turtle:
class Context
{
public:
Grid g;
Turtle t;
};
Analytic Geometry
Point
A point P in the plane can be represented by two reals (x, y) representing the x and y coordinates of P respectively. Complete the following C++ implementation of Point:
class Point
{
public:
Point(double x = 0, double y = 0);
double getxc() { return xc; }
double getyc() { return yc; }
ostream& print(ostream& os) const;
istream& read(istream& is);
void plot(Grid& g) const;
private:
double xc, yc;
};
Line
Any two points (x0, y0) and (x1, y1) on the plane determine a unique line l that passes through them. The slope, y-intercept, and equation of this line is determined by the equations:
slope = m = (y1 - y0)/(x1 - x0)
y-intercept = b = y0 - mx0
y = m * x + b
Two lines are parallel if their slopes are the same, but their y-intercepts are different. Two lines are equal if their slopes and y-intercepts are the same. Two lines are perpendicular if the product of their slopes is -1.
Complete the following C++ implementation of Line:
class Line {
public:
Line(Point p, Point q);
ostream& print(ostream& os) const;
istream& read(istream&);
void plot(Grid& g) const;
double yIntercept() const;
double xIntercept() const;
double slope() const;
bool isVertical() const;
bool is Horizontal() const;
Point intersction(const Line& l) const;
bool isParallel(const Line& l) const;
bool isPerpendicular(const Line& l) const;
private:
Point p1, p2;
double slope, yIntercept;
};
Test Harness
Implement a simple interpreter that perpetually prompts users for two lines, then displays the results produced by all of the functions defined above.